文系の皆さん、さようなら。どうも2回生漕手の榛澤です。タイトルは高校の時に書いた研究のタイトルです。同期のカンカンこと東村敢が趣味丸出しのブログを書いていたのを見て「自分も書こう」と思い立って早半年、3回目のブログ当番がついにやってきたので自分も高校時代を思いだしながら趣味の数学の話にふけりたいと思います。文系の皆様はここで読むのをやめてlearn to fly でも聞いててください。
PVはいいぞ。

話は高校時代にさかのぼります。当時数学研究会を立ち上げようと言っていた友人から研究会の実権を奪い取った僕は比較的たのしく問題を解きながら日々過ごしていました。そんな時、体育の帰りバスの中でふと以下の等式を思いつきました。
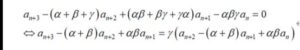
この等式自体は大したことはないのですが、(勘のいい人はお気づきでしょうが)一般化することができるとわかりました。つまり↓のように書けます。
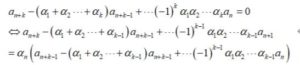
これをワチャワチャしてゴチャゴチャした結果、(k+1)項間漸化式の一般項がa1,a2..,a(k+1)と係数α1,α2..,α(k+1)を用いて表せるということがわかります。
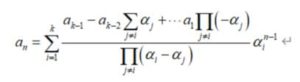
この応用から様々なことがわかりました。例えば、
応用その①「多項間漸化式の一般項が収束する⇔特性方程式の任意の解αが|α|<1を満たす」
応用その②「多項式を多項式で割ったときの商は割る側の多項式を特性方程式にもつ漸化式の項となる(初項は定める必要アリ)」
応用その③「多積間漸化式が解ける」
などなどです。僕的には①と③を導けたとき達成感があり、結構わかりやすい性質が出てきて面白かったです。当初は大学について全く知識がなかったので「これ大学入って論文とかに使えるんじゃね!?」とか思ってました。
こんなことをしている間に数学の先生に目を付けられ、当時出たばかりの特色入試とやらを受けることになりました。(部内にコレで受かった人が何人かいてマジか!?ってなりましたね笑)理学部はそれまで10倍だった倍率が17倍にまで跳ね上がり一次試験の時点で84人中71人が落とされるという鬼畜極まりない試験でしたが二時間で2完しパスすることができました。2次試験の面接の日に残り13人が一堂に会し、20分ほど怖い教授5人対自分一人で面接を受けました。当時は当然きづかなかったのですがそこには同期の田熊がいたのです!!!なんという偶然。

しかし某数学オリンピスト×3を筆頭とした上位層の人間にはなすすべもなく、僕と田熊はおとなしく一般入試を受け、無事通過して今に至ります。そんな僕たちも今や一回生の時に聞いたはずのGORILLAをまた聞き、ライリスの1000字レポートにおびえながら日々暮らしています。いったいどこで間違えたのでしょうか?まあ楽しいのでヨシ!ここらでブログを終わりたいと思います。僕個人として気になるので部員の人はドシドシ自分の今までのエピソードとかを書いてください。それでは~~
